How the Rating System Works
The rating system uses standard concepts and techniques from probability and statistics. This makes the rating system quite different from (and more accurate than) almost all other rating and ranking systems. The following is a nontechnical explanation of how the rating system works.
Basic Concepts
We presume that each player has a playing strength, i.e., a number that quantifies how strong the player is. The playing strength of a player does not change during a single event, but may change over time, as the player gets better or worse. (An event is a collection of matches, e.g., a tournament, that an event director submits to Ratings Central as a group.)
Even if we knew the playing strengths of two players, we would not know for certain which player would win, since a weaker player will sometimes beat a stronger player. A match is an upset if the player with the lower playing strength wins. We presume that the probability that a match will be an upset is determined solely by the difference in playing strengths of the two players. The larger the difference in the playing strengths, the more likely it is that the stronger player will win. The probability-of-upset function quantifies this.

There are two kinds of probability. There is the probability that one player will defeat another. (This probability is determined by the players’ playing strengths.) There is also the probability that a player’s playing strength is a certain value (e.g., 1106). The first probability is a property of the players, while the second probability is a property of the rating system.
Laws
The rating system does not know the playing strengths of players. It only sees match results. The rating system keeps track of what it knows about each player by constructing a law to describe the player’s playing strength.
A law is a probability distribution. The rating system assigns a law to each player. The player’s law describes the rating system’s knowledge of the playing strength of the player. This knowledge is derived from all the match results. The player’s law changes with every match that the rating system processes (because the rating system’s knowledge of the playing strength of the player changes with every match). From the law, we may determine the probability that the player’s playing strength is a certain value (e.g., 1106).
The mean of a law is essentially the location of the center of the law. The mean of a player’s law is the rating system’s best estimate of the player’s playing strength (because it is the center of the rating system’s knowledge of the player’s playing strength). The mean of a player’s law is the rating that the rating system outputs for the player.
The standard deviation measures the spread (width) of a law. The greater the standard deviation of a player’s law, the less certain the rating system is of the player’s playing strength. The probability that a player’s playing strength is within one standard deviation of the mean of the player’s law is approximately 68%. The probability that it is within two standard deviations is approximately 95%. The probability that it is within three standard deviations is approximately 99.7%.
If the meaning of a sentence like “The probability that a player’s playing strength is within two standard deviations is 95%.” isn’t clear, here is another way of saying the same thing: There is a 95% probability that the player’s playing strength is between the mean minus twice the standard deviation and the mean plus twice the standard deviation. For example, if the mean is 1106 and the standard deviation is 42, then
- There is a 68% probability that the player’s playing strength is between 1064 and 1148.
- There is a 95% probability that the player’s playing strength is between 1022 and 1190.
- There is a 99.7% probability that the player’s playing strength is between 980 and 1232.

Updates
A player’s playing strength may change over time, as the player gets better or worse. Because of this, the more time that has passed since the last event that the player played, the less certain we are of the player’s playing strength. The process of updating a player’s law to take into account the passage of time is the temporal update. The temporal update makes a law more spread out and slightly increases the mean. For example, if the rating system has not seen a player for a year, the standard deviation of the player’s law will increase by at most 79.4 points and the mean will increase by 7 points. However, the increase in mean will not be credited until the player plays in an event. (The temporal update is the sum of a mean-zero normal random walk with a variance of 70² per year and a Poisson jump process with jumps of 200 points, a mean of 7 points per year, and a variance of 200 × 7 per year. So, a player sometimes gets better or worse in steps and sometimes gets better in jumps.)

The process of updating a player’s law to take into account the player’s results in a single event is the event update. In theory, we should process all the results of an event as a single group. However, we need something that is computationally feasible. When doing the event update, the rating system only looks at a player’s results and the results of each of the player’s opponents. This is similar to what you might do at a tournament: Suppose that you lose a match and think your opponent is better than their rating. The way you might check this is to look at the draw sheets to see how your opponent did against other players. These are the same results that the rating system looks at when updating your rating.
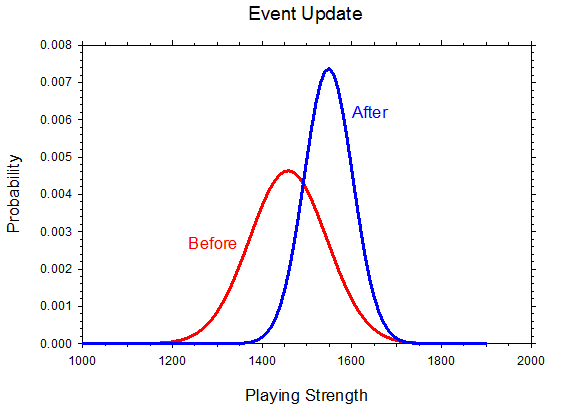
A small standard deviation makes it harder both to gain and to lose points. If a player with a small standard deviation plays a player with a large standard deviation, then the former’s rating will change less than the latter’s.
The rating system only cares about who wins a match, not what the score is.
New Players
The rating system assigns a law to each new (unrated) player. This law reflects what we expect the playing strength of a new player in the particular event to be. Event directors tell us what mean and standard deviation we should use for their event based on their experience. Event directors can also specify a law for a particular new player based on their knowledge of that player. Often, the standard deviation for a new player will be large reflecting the range in playing strength of unrated players that may enter the event. After playing an event or two, the standard deviation of a new player’s law should drop significantly. How quickly this happens depends on how many matches the player plays, the outcome of the matches, and the laws of the player’s opponents.

Event Processing
Here are the steps that the rating system goes through when processing an event:
- Assign a law to each unrated player.
- Retrieve the law of each rated player from the database and apply the temporal update.
- For each player:
- Calculate an adjusted law (defined below) for each of the player’s opponents.
- Update the player’s law for each of the player’s matches using in each case the adjusted law for the player’s opponent.
The adjusted law is the opponent’s law updated for all of the opponent’s matches except for the matches with the current player. The adjusted law depends on both the player and the opponent. So, the same opponent will have different adjusted laws when different players are being processed.
Summary Report
Here is a sample from a summary report for an event:
| ID | Name | Initial Rating | Point Change | Final Rating |
|---|---|---|---|---|
| 5766 | Bulatao, Jose G. | 1797±58 | −4 | 1793±52 |
| 5568 | Cembura, Julianne | 1500±450 | −539 | 961±246 |
| 7355 | Ching, Joe T. | 1984±38 | +2 | 1986±36 |
| 6655 | Chiu, David | 2050±66 | +20 | 2070±49 |
| 5925 | Collamore, Gil | 1121±95 | −126 | 995±59 |
| 5184 | Conley, Denny | 1463±38 | +19 | 1482±34 |
| 5044 | Cortesi, Tony | 1139±90 | −58 | 1081±54 |
The numbers after the plus/minus signs are the standard deviations of the laws. The initial-rating column contains the rating and standard deviation that the player had at the beginning of the event. For unrated players, this is from the law that the player is assigned. For rated players, it is from the result of applying the temporal update to the player’s final law from their previous event. The final-rating column contains the rating and standard deviation for the player after processing all the matches in the event. The value in the point-change column is the final rating minus the initial rating.
Detailed Report
Here is a sample from a detailed report for an event:
- Boulard, Claude
- Rating Change
1701±53 + 89 = 1790±40 - Wins
- Losses
- Point
Change - Opponent’s
Rating - Opponent
- Score
- Point
Change - Opponent’s
Rating - Opponent
- Score
- +36
- 1915±50
- Chen, Wei Teng
- −8 7 −6 8 9
- 0*
- 1812±34
- Bhatia, Sonu
- 8 9 4
- +14*
- 1812±34
- Bhatia, Sonu
- −8 −9 6 9 8
- −1
- 2016±48
- Maitra, Subhajit
- 7 −8 4 7
- +13*
- 1785±61
- Landsman, Alex
- −8 8 19 −5 11
- 0
- 2189±40
- Wang, Yin
- 8 −6 8 5
- +13*
- 1785±61
- Landsman, Alex
- −3 11 9 −9 9
- +10
- 1750±34
- Kalagher, Chris
- −10 11 8 9
- +3
- 1629±52
- Jordan, Kip
- 4 −6 3 9
- +2
- 1587±67
- Warrier, Sunil
- 10 7 7
- 0
- 1366±53
- Sharma, Rajeev
- 4 −7 4 −9 9
- Landsman, Alex
- Rating Change
1776±64 − 35 = 1741±54 - Wins
- Losses
- Point
Change - Opponent’s
Rating - Opponent
- Score
- Point
Change - Opponent’s
Rating - Opponent
- Score
- +9
- 1630±49
- Baird, Jim
- 8 8 5
- −22*
- 1761±43
- Boulard, Claude
- −3 11 9 −9 9
- −22*
- 1761±43
- Boulard, Claude
- −8 8 19 −5 11
- 0
- 2170±29
- Chui, Lim Ming
- 5 7 8
- Kalagher, Chris
- Rating Change
1752±37 − 7 = 1745±33 - Wins
- Losses
- Point
Change - Opponent’s
Rating - Opponent
- Score
- Point
Change - Opponent’s
Rating - Opponent
- Score
- +8
- 1753±50
- Baylies, Michael
- −5 3 9 8
- −8
- 1771±42
- Boulard, Claude
- −10 11 8 9
- +3
- 1625±52
- Jordan, Kip
- 9 5 5
- −6
- 1798±33
- Bhatia, Sonu
- 3 −6 11 9
- −5
- 1811±42
- Massarsky, Lev
- −10 9 6 9
- 0
- 2015±48
- Maitra, Subhajit
- 6 4 6
- 0
- 2189±40
- Wang, Yin
- 5 9 8
The top section of each table contains the player’s name. In the top section under the line “Rating Change” is the player’s initial rating and standard deviation, the point change for the player for the event, and, after the equals sign, the player’s final rating and standard deviation. Below this are the player’s wins and losses.
The value in the “Opponent’s Rating” column is the mean and standard deviation of the opponent’s adjusted law. As mentioned above, the rating system uses different adjusted laws for the same opponent when processing different players, e.g., Claude Boulard’s adjusted rating was 1761±43 when he played Alex Landsman, but 1771±42 when he played Chris Kalagher.
The value in the “Point Change” column is the point change for the player for that result. However, the rating system processes multiple matches between the same two players as a unit. In such a case, the total point change for all the matches between the two players is distributed among the matches between the two players as follows:
- If the total point change is positive (or zero), then the total point change is distributed equally among the matches that the player won, and the point change for each match that the player lost is zero.
- If the total point change is negative, then the total point change is distributed equally among the matches that the player lost, and the point change for each match that the player won is zero.
If the two players played more than one match with each other, there will be an asterisk after the point change value. For example, Claude Boulard gained 14 points total for his one win and one loss to Sonu Bhatia and gained 26 points total for his two wins over Alex Landsman.
The point change per match depends on the order that the rating system processes the matches. So, the values reported as the point change per match are merely suggestive. However, the sum of the per-match point changes equals the total point change for the player for the event, and this total does not depend on the order that the rating system processes the matches.
The dependence of the point change per match on the processing order makes intuitive sense: Suppose that we see a 2000 player defeat a 2200 player. We will significantly increase our estimate of the rating of the 2000 player. Now, suppose that we see the same player defeat another 2200 player. We will again increase our estimate of the player’s rating, but not by as much as we did before.
To make the detailed report easier to understand, the matches are processed in the following order: First the losses in increasing order of the opponent’s rating, then the wins in decreasing order of the opponent’s rating. If the player has both a win and a loss against an opponent, then if the opponent’s rating is higher, those matches will be sorted as a win, otherwise as a loss.
The number of points gained by the winner of a match will hardly ever equal the number of points lost by the loser of a match. For example, Claude Boulard gained a total of 26 points for his two wins over Alex Landsman, but Alex lost 44 points for the same two matches. In this case, Alex lost more points because Alex’s standard deviation was larger and Alex and Claude’s means were similar after processing the other matches that they played.
Since the point change values are rounded to the nearest integer for displaying, occasionally the sum of the per-match point changes will not equal the total point change for the player for the event. If there is a discrepancy, it will usually be only a point.
References
Marcus, David J. (2001) New Table-Tennis Rating System. Journal of the Royal Statistical Society: Series D (The Statistician), 50: 191–208. doi: 10.1111/1467-9884.00271
Marcus, David J. (2011a) Ratings Central: Accurate, Automated, Bayesian Table Tennis Ratings for Clubs, Leagues, Tournaments, and Organizations. Joint Statistical Meetings, July 30–August 4, 2011.
Marcus, David J. (2011b) Ratings Central: Accurate, Automated, Bayesian Table Tennis Ratings for Clubs, Leagues, Tournaments, and Organizations. NESSIS (New England Symposium on Statistics in Sports), September 24, 2011.
Marcus, David J. (2023) Long-Term Stable, Quick-Reacting Table Tennis Ratings via Poisson Jumps. September 24, 2023; revised July 27, 2025.

