このレイティングシステムのしくみ
Ratings Centralのシステムは、確率統計学の分野で広く認められた理論と手法に基づいています。その点で他のほとんどのレイティングやランキングのシステムとはかなり異なっています。結果として、このシステムはより正確にプレイヤーの強さを推定することができます。以下では、このレイティングシステムのしくみをなるべく専門的にならないように解説します。
基礎にある考え方
まず、それぞれのプレイヤーは、一つの数で表される「卓球の強さ」を持つと仮定します。それは、各プレイヤーが実際にどれくらい強いのかを示す数値です。「卓球の強さ」は、そのプレイヤーが上手くなったり下手になったりするにつれて時間とともに変化すると考えます。ただし、一つのイベント中には変化しないものとします。(ここで「イベント」とは、複数の試合から構成される大会のようなものを表します。イベント運営者はそのイベント毎に試合結果をひとまとめにしてRatings Centralに提出します。)
[訳注] プレイヤーの「卓球の強さ」は直接知ることができない隠れた情報です。これがそのままレイティングに対応するわけではありません。このシステムは、この隠れた情報を、外から見える情報である試合の勝敗結果を使って推定します。そして、プレイヤーの真の卓球の強さを最もよく表すと推定される値が、そのプレイヤーのレイティングになります。
[訳注] Ratings Centralのイベントという用語は、日本語の「大会」とほぼ同義です。大会運営者は、その大会の全部の試合結果をまとめて提出します。ただし、大会が男女別にはっきり分かれていて互いの対戦がない場合などには、男女を別のイベントとして提出することもできます。Ratings Centralのイベント一覧には、このイベント単位で結果が表示されます。
さて、二人のプレイヤーの卓球の強さが分かっていたとしても、どちらが勝つかを確実に知ることは不可能です。なぜなら、弱い方のプレイヤーが強い方のプレイヤーに勝つことも時々は起きるからです。弱い方が強い方に勝った試合のことを「番狂わせ」と呼ぶことにします。このレイティングシステムでは、「番狂わせ」が起きる確率は二人のプレイヤーの卓球の強さの差だけで決まると仮定します。二人の差が大きいほど、強い方のプレイヤーが勝つ可能性が高くなります。この確率を「番狂わせ確率関数」で表します。

[訳注] この関数は、BradleyとTerryによる1952年の論文で示された一対比較のモデルと同様の式を用いています。グラフから分かるように、強さの差が0の場合はどちらが勝つか五分五分であり、強さの差が大きくなるほど番狂わせが起きる確率が下がります(つまり強い方が順当に勝つ可能性が高くなる)。差がいくらの時にどれくらいの確率で番狂わせが起きるかというパラメータは、アメリカ卓球協会のデータを使って、過去に行われた試合の勝敗を最もよく推定できるように決めています。
説明の中で、二種類の確率の話が出てきますので注意してください。一つは、あるプレイヤーが別のプレイヤーに勝つ確率です(二人のプレイヤーの卓球の強さで決まります)。もう一つは、あるプレイヤーの卓球の強さを、(例えば 1106 というような)ある特定の数値で表すことがどれくらいもっともらしいかという確率です。前者は、プレイヤーに関する情報であり、後者はこのレイティングシステムの属性です。
ロウ
レイティングシステムは、各プレイヤーが実際にどれくらい強いのかを知りません。試合の結果だけから判断します。システムは、プレイヤーの卓球の強さに関する情報を管理するために、それぞれのプレイヤーの卓球の強さがどれくらいであるかを示す「ロウ」を使います。
[訳注] 原文で使われているlawという単語は一般的には「法則」などと訳されますが、ここでは確率の用語として特別な意味で使用しているため、そのままカタカナの「ロウ」としました。
このレイティングシステムは、一人一人のプレイヤーにそれぞれのロウを割り当てます。プレイヤーのロウとは、そのプレイヤーの卓球の強さに関して、このシステムが知っている知識です。この知識は全ての試合結果に基づいて決まります。あるプレイヤーの卓球の強さに関してシステムが知っている知識は、試合毎に更新されていくので、プレイヤーに当てはめられたロウも、システムが試合結果を処理するたびに変化します。このロウを使うと、あるプレイヤーの卓球の強さが(例えば1106のような)ある特定の数値である確率を求めることができます。
ロウの「平均値」とは、(おおまかな言い方ですが)ロウの中心の値のことです。プレイヤーのロウの平均値が、このシステムがそのプレイヤーの卓球の強さを推定した時に最も正しいと考えられる値になります。レイティングシステムがそのプレイヤーの卓球の強さに関して知っているのはそのロウだけであり、その中心で確率が最大になるからです。プレイヤーのロウの平均値が、システムが計算するそのプレイヤーのレイティングになります。
ロウの「標準偏差」は、ロウの広がり(幅)を表します。プレイヤーのロウの「標準偏差」が大きいほど、システムはそのプレイヤーの卓球の強さに関して確信がないということを意味します。プレイヤーの卓球の強さが、そのプレイヤーのロウの平均値から±標準偏差の範囲にある確率はおよそ68%になります。参考までに、±標準偏差×2の範囲にある確率はおよそ95%、±標準偏差×3の範囲にある確率はおよそ99.7%です。
「あるプレイヤーの卓球の強さが±標準偏差×2の範囲にある確率は95%です」というのは「プレイヤーの卓球の強さが(平均値-標準偏差×2)と(平均値+標準偏差×2)の間にある確率が95%」ということなので、例えばもしあるプレイヤーのロウの平均値が1106で標準偏差が42だとすると以下のようになります。
- そのプレイヤーの卓球の強さが1064〜1148である確率は68%。
- そのプレイヤーの卓球の強さが1022〜1190である確率は95%。
- そのプレイヤーの卓球の強さが980〜1232である確率は99.7%。

ロウの更新
プレイヤーは時間とともに上手くなったり下手になったりします。つまり、その卓球の強さが時間とともに変わります。そのため、あるプレイヤーが試合をした最後のイベントから時間が経つと、システムが持つそのプレイヤーの卓球の強さに関する知識の確信度は下がっていきます。経過時間に基づいてロウを更新する処理を「経過時間更新」と呼びます。経過時間更新によって、ロウの広がりが大きくなり、平均値が少し増加します。例えば、あるプレイヤーの試合に関する情報が1年間システムに入力されなかったとすると、そのプレイヤーのロウの標準偏差は最大で79.4だけ増加し、平均値は7だけ増加します。ただし、平均値の増加分は、そのプレイヤーが次のイベントに参加するまではレイティングに反映されません。(より正確に説明すると、時間更新は、ゼロを平均とし1年あたりの分散が70²である正規ランダムウォークと、大きさが200ポイントで1年あたりの平均と分散がそれぞれ7と200 × 7であるポアソンジャンプ過程との和になっています。つまり、プレイヤーは徐々に強くなったり弱くなったりすると同時に、時々不連続に上達することがあるという考えです。)
[訳注] プレイヤーが試合に出ていない期間が続くと、新しい情報が入ってこないので、システムはそのプレイヤーに関する知識の確信度を下げていきます。

イベントでの試合結果に基づいてプレイヤーのロウを更新する処理を「イベント更新」と呼びます。あるプレイヤーのロウの更新を厳密に行うには、理論的には一つのイベントの(そのプレイヤーが出てない試合も含めて)全ての試合を一度に処理する必要があるのですが、計算を不要に複雑にしないために、このシステムではそのプレイヤーの試合結果とそのプレイヤーの対戦相手の試合結果だけを使って計算します。あなたも実際の大会で、同じようなことをやっているかもしれません。試合で誰かに負けた時、その相手は(事前に思っていたよりも)けっこう強かったんじゃないかなと考えますよね。そうすると、その相手が他の人と対戦した結果をチェックして、あの人にも勝っているし、やはり強いんだな、という風に納得したりします。レイティングシステムが個々のプレイヤーのレイティングを計算する時も、それと似たやり方で試合結果を調べます。
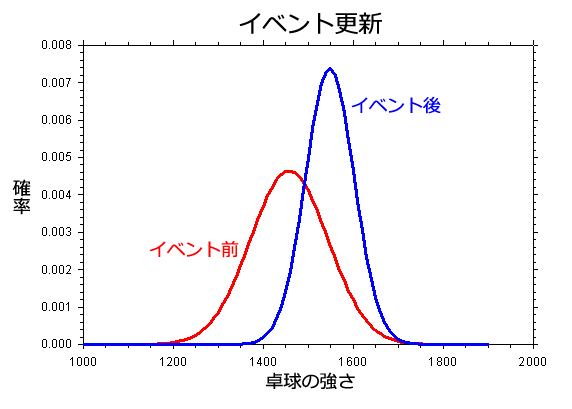
標準偏差が小さいと、レイティングが増減しにくくなります。標準偏差の小さいプレイヤーと標準偏差の大きいプレイヤーが試合をした場合、標準偏差の大きいプレイヤーのレイティングの変化の方が標準偏差の小さいプレイヤーの変化よりも大きくなります。
[訳注] このしくみがない場合、あまり試合に出ていないためにレイティングが実際の実力以上に高目に計算されてしまっているプレイヤーに勝ったり、逆に実際の実力以下に低めに計算されてしまっているプレイヤーに負けたりすると、レイティングが実際以上に大きく変化してしまいます。そのような不正確なレイティングの変化は、次の対戦相手である他のプレイヤーに伝播していき、結果として全てのプレイヤーのレイティングを不正確にしてしまいます。
このレイティングシステムは試合の勝敗のみを使って計算し、点差などは考慮しません。
[訳注] つまり、ボールの威力やサーブの種類の豊富さなどは当然のこと、試合の最終的なゲームカウントやスコアも考慮されません。それらの情報がある程度プレイヤーの強さを反映していることは事実でしょう。しかし、例えば、1ゲームあるいは1点の重みは、状況やプレイヤー自身の戦略によっても変わるので、実際にどのように強さの推定に使えるかについて、理論的裏付けがありません。そのような情報を使うと推定結果を逆に不正確にすることになります。
初めてレイティングに参加するプレイヤーの扱い
システムは初参加の(まだレイティングの無い)プレイヤー達に新規にロウを割り当てます。この初参加プレイヤー達のためのロウは、そのイベントに参加するレイティングの無いプレイヤー達がおよそどれくらいの平均値と標準偏差を持つかを定めたもので、イベントの運営者が決めることになります。何らかの事前情報があれば、特定のプレイヤーについてはそのプレイヤー用のロウを初期値として与えることもできます。たいていの場合、初参加プレイヤーに割り当てるロウの標準偏差は大きい値にします。これはそのイベントに参加する初参加プレイヤー達の強さの範囲を反映させるためです。そのプレイヤーが一つか二つのイベントに参加すると、標準偏差は急激に小さくなります。ただし、どれくらい急激に小さくなるかは、そのプレイヤーが試合をした数と、試合結果と、対戦したプレイヤー達のロウによって変わります。

[訳注] 初参加のプレイヤーの強さを見積ることが難しい場合は、上のグラフの平たく広がったロウのように大きい標準偏差のロウを割り当てます。このようなロウは試合結果によって大きく平均値が変動することができるので、ロウの初期平均値からの強い影響を避けることができ、少ない試合回数で正確なレイティングに近づいていきます。
イベントの処理
レイティングシステムのイベント処理は以下のような流れで行われます。
- まだレイティングのないプレイヤーに初参加プレイヤー用のロウを割り当てる。
- 既にレイティングのあるプレイヤーのロウを経過時間更新処理で更新する。
- 全てのプレイヤー対して:
- プレイヤーが対戦した相手プレイヤーの一人一人について、補正ロウ(下で説明)を求める。
- プレイヤーのロウをそのプレイヤーがプレイしたそれぞれの試合結果に基づいて更新する。この時、更新の計算にはその試合の相手プレイヤーの補正ロウを用いる。
ここで「補正ロウ」というのは、一人の対戦相手のロウを現在のプレイヤーとの試合以外の結果を使って更新したものになります。補正ロウはプレイヤーと相手プレイヤーの両方に依存するので、誰の対戦相手として処理しているかによって、同じプレイヤーは異なる補正ロウを持つことになります。
サマリーレポート
イベントのサマリーレポートの例はこのようなものです。
| ID | Name | Initial Rating | Point Change | Final Rating |
|---|---|---|---|---|
| 5766 | Bulatao, Jose G. | 1797±58 | −4 | 1793±52 |
| 5568 | Cembura, Julianne | 1500±450 | −539 | 961±246 |
| 7355 | Ching, Joe T. | 1984±38 | +2 | 1986±36 |
| 6655 | Chiu, David | 2050±66 | +20 | 2070±49 |
| 5925 | Collamore, Gil | 1121±95 | −126 | 995±59 |
| 5184 | Conley, Denny | 1463±38 | +19 | 1482±34 |
| 5044 | Cortesi, Tony | 1139±90 | −58 | 1081±54 |
プラスマイナス記号の後の数値はロウの標準偏差です。Initial Rating(元のレイティング)の項は、このイベントの直前のプレイヤーのレイティングと標準偏差です。これは、初参加のプレイヤーの場合はイベント運営者が決めた初期ロウで、それ以外のプレイヤーの場合はそのプレイヤーが最後に参加したイベントで計算されたロウに経過時間更新を加えたものになります。Final Rating(最終レイティング)の項は、イベントの全ての試合が処理された後のプレイヤーのレイティングと標準偏差です。Pint Change(増減)の項は、最終レイティングから元のレイティングを引いた値です。
詳細レポート
イベントの詳細レポートの例はこのようなものです:
- Boulard, Claude
- Rating Change
1701±53 + 89 = 1790±40 - Wins
- Losses
- Point
Change - Opponent’s
Rating - Opponent
- Score
- Point
Change - Opponent’s
Rating - Opponent
- Score
- +36
- 1915±50
- Chen, Wei Teng
- −8 7 −6 8 9
- 0*
- 1812±34
- Bhatia, Sonu
- 8 9 4
- +14*
- 1812±34
- Bhatia, Sonu
- −8 −9 6 9 8
- −1
- 2016±48
- Maitra, Subhajit
- 7 −8 4 7
- +13*
- 1785±61
- Landsman, Alex
- −8 8 19 −5 11
- 0
- 2189±40
- Wang, Yin
- 8 −6 8 5
- +13*
- 1785±61
- Landsman, Alex
- −3 11 9 −9 9
- +10
- 1750±34
- Kalagher, Chris
- −10 11 8 9
- +3
- 1629±52
- Jordan, Kip
- 4 −6 3 9
- +2
- 1587±67
- Warrier, Sunil
- 10 7 7
- 0
- 1366±53
- Sharma, Rajeev
- 4 −7 4 −9 9
- Landsman, Alex
- Rating Change
1776±64 − 35 = 1741±54 - Wins
- Losses
- Point
Change - Opponent’s
Rating - Opponent
- Score
- Point
Change - Opponent’s
Rating - Opponent
- Score
- +9
- 1630±49
- Baird, Jim
- 8 8 5
- −22*
- 1761±43
- Boulard, Claude
- −3 11 9 −9 9
- −22*
- 1761±43
- Boulard, Claude
- −8 8 19 −5 11
- 0
- 2170±29
- Chui, Lim Ming
- 5 7 8
- Kalagher, Chris
- Rating Change
1752±37 − 7 = 1745±33 - Wins
- Losses
- Point
Change - Opponent’s
Rating - Opponent
- Score
- Point
Change - Opponent’s
Rating - Opponent
- Score
- +8
- 1753±50
- Baylies, Michael
- −5 3 9 8
- −8
- 1771±42
- Boulard, Claude
- −10 11 8 9
- +3
- 1625±52
- Jordan, Kip
- 9 5 5
- −6
- 1798±33
- Bhatia, Sonu
- 3 −6 11 9
- −5
- 1811±42
- Massarsky, Lev
- −10 9 6 9
- 0
- 2015±48
- Maitra, Subhajit
- 6 4 6
- 0
- 2189±40
- Wang, Yin
- 5 9 8
それぞれのテーブルの上部には、まずプレイヤーの名前が記載されています。続くRating Changeの欄に表示されているのは、そのプレイヤーの元のレイティングと標準偏差、レイティングの増減、そしてイコール記号の後が最終レイティングとその標準偏差です。テーブルの下部には、勝ちと負けの結果が記載されています。
Opponent’s Rating(対戦相手のレイティング)の項の値は対戦相手の補正ロウの平均値と標準偏差です。上で説明したように、どのプレイヤーを処理しているかによって、同じ選手に対しても異なる補正ロウが使われます。例えば、Claude Boulardの補正ロウは、Alex Landsmanとの対戦表では1761±43ですが、Chris Kalagherとの対戦表では1771±42になります。
Point Change(増減)の項の値は、その試合の結果生じたレイティングの増減です。一つのイベント中に同じ二人の選手が複数回試合した場合、システムはその複数回の試合を一度に処理し、その二人の選手間の全ての試合結果から求めた増減の総和を、各試合に以下のように割り振ります。
- もし増減の総和が0以上の場合、勝った試合に均等に割り振り、負けた試合での増減は0と表示されます。
- もし増減の総和がマイナスの場合、負けた試合に均等に割り振り、勝った試合での増減は0と表示されます。
二人のプレイヤーが複数回試合をした場合、増減の値にアステリスクが表示されます。例えば、Claude Boulardは、Sonu Bhatiaと二回試合をして一勝一敗、トータルで14だけレイティングが増加し、Alex Landsmanとも二回試合をして二勝、トータルで26だけレイティングが増加しました。
[訳注] アステリスクは、この増減がこの欄の試合だけで決まったのではないですよ、という意味だと考えてください。
個々の試合毎の増減の値はシステムが各試合を処理する順序によって多少変動します。その意味で、試合毎の個々の増減の値は参考と考えてください。試合毎の増減を全て合計すると、そのイベントでのそのプレイヤーのレイティングの増減になります。この総和の値はシステムが処理する順番に依存せず、試合の結果から一意に決まります。
処理の順序にって試合毎の増減値が変動するというのはやや分かりにくいですが、次のように考えれば直感的に理解できるかもしれません。例えば、レイティングが2000であるプレイヤーが、レイティングが2200のプレイヤーに勝ったとします。システムはこの試合の結果から2000のプレイヤーのレイティングを大きく増加させることになります。ここで、同じこのプレイヤーが、別の2200のプレイヤーにも勝っているとします。システムはまたレイティングを増加させますが、さっきの試合の処理をした時ほどは増加させないことになります。
[訳注] その結果、同じ2200のプレイヤーとの対戦であるにもかかわらず、先に処理した試合での増減が大きい値になります。
試合が次の順序で処理されることに注意すると、詳細レポートを理解しやすいでしょう。まず、負けた試合が対戦相手のレイティングの低い順に処理されます。次に、勝った試合が対戦相手のレイティングの高い順に処理されます。同じ対戦相手と複数回対戦して勝ちと負けの両方がある時は、もしその対戦相手のレイティングが自分より高い場合は、その全試合とも自分が勝った試合とみなされ、逆に相手の方が低い場合は、全て負けた試合とみなされた上で、先の順序が適用されます。
一つの試合の勝者の増加値と敗者の減少値は、ほとんどの場合異なる値になります。例えば、Claude BoulardはAlex Landsmanと二試合し、合計26だけ増加しましたが、同じ二試合でAlexは44だけ減少しました。他の試合を処理した後の二人の平均値はよく似た値でしたが、Alexの標準偏差の方が大きかっために、Alexが失った値の方が大きくなります。
表示では小数点以下をまるめて整数として表示しているので、個々の試合での増減の合計が、イベント全体でのレイティングの増減とぴったり一致しない場合があります。誤差があったとしても通常は1ポイントだけです。
参考文献
Marcus, David J. (2001) New Table-Tennis Rating System. Journal of the Royal Statistical Society: Series D (The Statistician), 50: 191–208. doi: 10.1111/1467-9884.00271
Marcus, David J. (2011a) Ratings Central: Accurate, Automated, Bayesian Table Tennis Ratings for Clubs, Leagues, Tournaments, and Organizations. Joint Statistical Meetings, July 30–August 4, 2011.
Marcus, David J. (2011b) Ratings Central: Accurate, Automated, Bayesian Table Tennis Ratings for Clubs, Leagues, Tournaments, and Organizations. NESSIS (New England Symposium on Statistics in Sports), September 24, 2011.
Marcus, David J. (2023) Long-Term Stable, Quick-Reacting Table Tennis Ratings via Poisson Jumps. September 24, 2023; revised July 27, 2025.
日本語版文責: 仁科繁明

