Como trabaja el Sistema de Rating
El sistema de rating usa conceptos y técnicas que son basadas en las leyes de probabilidad y estadística. El uso de estas técnicas hace de este sistema muy diferente a cualquier otro sistema de rating. Lo que sigue es una explicación sencilla (no técnica) de como trabaja el sistema de rating.
Conceptos Básicos
Primero asumimos que cada jugador posee una cierta destreza en su nivel de juego. Esta destreza en el nivel de juego es representado por un número que cuantifica la destreza del jugador. El nivel de juego de un jugador no cambia durante un evento o torneo, pero quizás cambie a través del tiempo, a medida que el jugador mejora o empeora en su nivel de juego. (Un evento es una colección de partidos que el coordinador del evento o torneo envía a Ratings Central como grupo.)
Aunque conocemos de ante manos el nivel de juego de dos jugadores, no sabemos de cierto que jugador va a ganar el partido ya que un jugador inferior ocasionalmente puede ganarle a un jugador superior. Un partido con el resultado inesperado se define cuando el jugador con un nivel de juego más bajo que su contrincante gana el partido. Aquí asumimos que la probabilidad que un partido resulte en un resultado inesperado se determina solamente por la magnitud de la diferencia en el nivel de juego de los dos jugadores. Cual mayor es esta diferencia de los niveles de juego, lo más probable es que el jugador de más alto nivel gane el partido. La función de probabilidad de un resultado inesperado cuantifica esto.
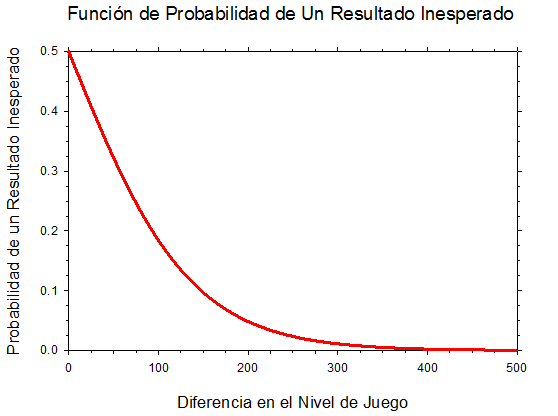
Existen dos clases de probabilidades. Hay una probabilidad de que un jugador derrote a otro. (Esto se determina por la diferencia en el nivel de rating entre los jugadores). También existe la probabilidad de que el nivel de juego de cada jugador sea de cierto valor (o sea 1106). O sea el valor verdadero del rating que un jugador posee es incierto. La primera probabilidad es la propiedad de los jugadores, la segunda probabilidad es la propiedad del sistema de rating.
Leyes de Probabilidad
El sistema de rating no conoce el nivel de juego de los jugadores. El sistema trata de estimar el nivel usando los resultados de los partidos entre los jugadores de un evento o torneo. (El sistema solamente considera los resultados de los partidos.) El sistema mantiene un historial de los resultados de los partidos de cada jugador creando asi una ley de probabilidad que describe el nivel de juego del jugador.
Una ley es una distribución de probabilidades. El sistema de rating asigna una ley a cada jugador. Esta ley refleja el conocimiento del sistema de rating sobre el nivel de juego del jugador. Este conocimiento se obtiene procesando todos los resultados de los partidos del jugador y la de los contrincantes. La ley del jugador cambia con cada partido que el participa. El sistema de rating procesa los datos de los resultados de cada partido y así mejora el conocimiento sobre el rating de cada jugador. Con cada partido, el sistema aprende algo nuevo sobre cada jugador. Usando esta ley, podemos determinar la probabilidad de que el nivel de juego del jugador es de cierto valor (por ejemplo 1106).
La media de la ley es esencialmente el punto central de la ley. La media de la ley de un jugador es el mejor estimado del sistema de rating sobre el nivel de destreza del jugador (ya que es el centro del conocimiento que tiene el sistema de rating sobre el nivel de destreza del jugador). La media de la ley de un jugador es el rating que el sistema produce para el jugador.
La desviación estándar mide la confianza que tiene el sistema sobre el número generado de rating del jugador. Esto es medido por la dispersión o variabilidad de la ley de probabilidad del jugador. Mientras más alto es el valor de la desviación estándar, lo menos seguro esta el sistema del rating verdadero del jugador. La probabilidad que el nivel de juego esta dentro de una (1) desviación estándar de la media es el 68%. La probabilidad que esta dentro de 2 desviaciones estándar es 95%. La probabilidad que esta dentro de 3 desviaciones estándar es 99.7%.
Si esto no esta claro, aquí esta otra manera de decir lo mismo. Con una probabilidad de 95% podemos decir que el rating verdadero actual del jugador esta entre su media más y menos de dos desviaciones estándar. Por ejemplo, si la media del rating de un jugador es 1106 y la desviación estándar es de 42, entonces:
- Hay una probabilidad de 68% que el verdadero nivel de juego del jugador (o su rating verdadero actual) está entre 1064 y 1148.
- Hay una probabilidad de 95% que el verdadero nivel de juego del jugador (o su rating actual) está entre 1022 y 1190.
- Hay una probabilidad de 99.7% que el verdadero nivel de juego del jugador (o su rating actual) está entre 980 y 1232.

Actualización
El nivel de juego de un jugador puede cambiar a través del tiempo, a medida que el jugador mejore o empeore su nivel de juego. Por esto, mientras más tiempo haya pasado desde el último partido que el jugador haya jugado, lo menos cierto estamos de su verdadero nivel de juego. Este proceso de actualizar la ley del jugador dependiendo del tiempo desde su último partido se llama actualización temporal. La actualización temporal hace que la ley se extienda mas y aumenta la media ligeramente. Por ejemplo, si el sistema de rating no ha recibido información de un jugador por un año, la desviación estándar de la ley del jugador aumentaría por un máximo de 79.4 puntos y la media aumentaría por 7 puntos. Sin embargo, el aumento de la media no seria aplicada hasta que el jugador participe en un evento. (La actualización temporal es la suma de una caminata (paseo) aleatoria con una media de cero del 70² por año y un salto en el proceso Poisson con saltos de 200 puntos, y una media de 7 puntos por año, y una varianza de 200 × 7 por año.) Así que el jugador a veces mejora o empeora en pasos y a veces mejora en saltos.
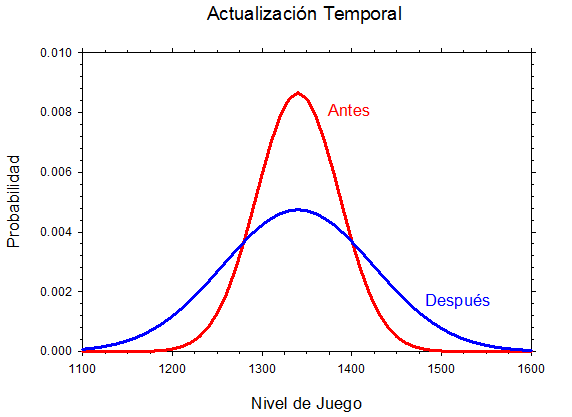
El proceso de actualizar la ley del jugador para tomar en cuenta los resultados del jugador en un evento o torneo se llama actualización del evento. En teoría, nosotros debemos procesar todos los resultados de los partidos de un evento juntos en un grupo. Sin embargo, esto es casi imposible para la computadora procesar; entonces hay que simplificar el proceso. Cuando se hace la actualización de un evento, el sistema de rating solo considera los resultados del jugador y también los resultados de cada uno de los contrincantes. Esto es similar a lo que Usted haría en un torneo: Suponga que usted pierde un partido contra un contrincante y piensa que el rating de su contrincante es mejor que su propio rating. La manera que Usted verificaría el rating de su contrincante es de ver los resultados de todos los otros partidos que jugo su contrincante para asi tener un estimado del verdadero nivel de juego de su contrincante. Estas son las mismas reglas que el sistema de rating usa cuando actualiza el rating de un jugador.

Si un jugador tiene una desviación estándar pequeña entonces a este le dificulta ganar y perder puntos. Si un jugador con una desviación estándar pequeña juega con otro jugador con una desviación estándar más alta, entonces el rating del primero cambia menos que la del segundo.
El sistema de rating solo le importa la decisión del partido (o sea quien gana y pierde), no cual es la puntuación del partido.
Nuevos Jugadores
El sistema de rating asigna una ley para nuevos jugadores (que no tienen rating en el sistema) Esta ley anticipa el nivel de juego del nuevo jugador en un evento. Generalmente, el director o coordinador del evento conoce la destreza del nuevo jugador y le asigna una media y una desviación estándar basada en su experiencia directa con el nuevo jugador. Si el coordinador no posee gran conocimiento sobre el jugador, entonces la desviación estándar asignada seria grande, así reflejando la gran incertidumbre que el sistema tiene sobre el rating verdadero de el nuevo jugador. Después de jugar uno o dos juegos, el sistema adquiere más confianza sobre el verdadero rating del nuevo jugador, y la desviación estándar del nuevo jugador comienza a bajar de valor. Que rápido esto sucede depende de cuantos partidos el nuevo jugador juega en un torneo, el ganador y perdedor de cada partido, y las leyes de rating de los jugadores contrincantes.

Procesamiento de Datos para un Evento
Estos son los pasos que sigue el sistema rating para procesar los datos de un evento:
- Asigna una ley para cada jugador nuevo (sin rating en el sistema).
- Extrae de la base de datos del sistema la ley de rating de cada jugador y aplica la actualización temporal.
- Para cada jugador en el evento:
- Calcula la ley ajustada (se define abajo) para cada contrincante del jugador
- Actualiza la ley del jugador para cada partido, usando en cada caso la ley de ajuste para cada jugador contrincante.
La ley de ajuste es la ley del jugador contrincante actualizada con los resultados de todos los partidos jugados por el contrincante contra otros en el evento; se excluyen los partidos con el jugador siendo clasificado. La ley de ajuste depende de ambos: el jugador siendo clasificado y de cada contrincante que el juega. Así que, el mismo contrincante tiene leyes de ajuste diferentes dependiendo del jugador siendo procesado por el sistema.
Resumen Final del Evento
Aquí mostramos un ejemplo del Resumen Final del Evento generado por el sistema para un evento:
| ID | Name | Initial Rating | Point Change | Final Rating |
|---|---|---|---|---|
| 5766 | Bulatao, Jose G. | 1797±58 | −4 | 1793±52 |
| 5568 | Cembura, Julianne | 1500±450 | −539 | 961±246 |
| 7355 | Ching, Joe T. | 1984±38 | +2 | 1986±36 |
| 6655 | Chiu, David | 2050±66 | +20 | 2070±49 |
| 5925 | Collamore, Gil | 1121±95 | −126 | 995±59 |
| 5184 | Conley, Denny | 1463±38 | +19 | 1482±34 |
| 5044 | Cortesi, Tony | 1139±90 | −58 | 1081±54 |
Los numeros que sigue el signo de sumar/restar son la desviaciónes estándar de la leyes de los jugadores. La columna llamada «Initial Rating» contiene el rating y la la desviación estándar que el jugador tiene a principio del evento. Para los jugadores sin rating, estos numeros vienen de la ley asignada al jugador. Para los jugadores con rating, estos numeros vienen de el resultado de aplicar la actualización temporal a la ley final del evento previo. La columna llamada «Final Rating» contiene el rating y la desviación estándar del jugador a la conclusión del evento después de procesar todos los partidos del evento. El valor en la columna llamada «Point Change» es la diferencia entre el rating final y el rating inicial.
Informe Detallado
Aquí le mostramos un ejemplo del Informe Detallado de un evento
- Boulard, Claude
- Rating Change
1701±53 + 89 = 1790±40 - Wins
- Losses
- Point
Change - Opponent’s
Rating - Opponent
- Score
- Point
Change - Opponent’s
Rating - Opponent
- Score
- +36
- 1915±50
- Chen, Wei Teng
- −8 7 −6 8 9
- 0*
- 1812±34
- Bhatia, Sonu
- 8 9 4
- +14*
- 1812±34
- Bhatia, Sonu
- −8 −9 6 9 8
- −1
- 2016±48
- Maitra, Subhajit
- 7 −8 4 7
- +13*
- 1785±61
- Landsman, Alex
- −8 8 19 −5 11
- 0
- 2189±40
- Wang, Yin
- 8 −6 8 5
- +13*
- 1785±61
- Landsman, Alex
- −3 11 9 −9 9
- +10
- 1750±34
- Kalagher, Chris
- −10 11 8 9
- +3
- 1629±52
- Jordan, Kip
- 4 −6 3 9
- +2
- 1587±67
- Warrier, Sunil
- 10 7 7
- 0
- 1366±53
- Sharma, Rajeev
- 4 −7 4 −9 9
- Landsman, Alex
- Rating Change
1776±64 − 35 = 1741±54 - Wins
- Losses
- Point
Change - Opponent’s
Rating - Opponent
- Score
- Point
Change - Opponent’s
Rating - Opponent
- Score
- +9
- 1630±49
- Baird, Jim
- 8 8 5
- −22*
- 1761±43
- Boulard, Claude
- −3 11 9 −9 9
- −22*
- 1761±43
- Boulard, Claude
- −8 8 19 −5 11
- 0
- 2170±29
- Chui, Lim Ming
- 5 7 8
- Kalagher, Chris
- Rating Change
1752±37 − 7 = 1745±33 - Wins
- Losses
- Point
Change - Opponent’s
Rating - Opponent
- Score
- Point
Change - Opponent’s
Rating - Opponent
- Score
- +8
- 1753±50
- Baylies, Michael
- −5 3 9 8
- −8
- 1771±42
- Boulard, Claude
- −10 11 8 9
- +3
- 1625±52
- Jordan, Kip
- 9 5 5
- −6
- 1798±33
- Bhatia, Sonu
- 3 −6 11 9
- −5
- 1811±42
- Massarsky, Lev
- −10 9 6 9
- 0
- 2015±48
- Maitra, Subhajit
- 6 4 6
- 0
- 2189±40
- Wang, Yin
- 5 9 8
La sección titular (de arriba) de cada tabla contiene el nombre del jugador. En la sección de arriba debajo de la línea titulada «Rating Change» (Cambio de Rating) esta el rating inicial del jugador junto a la desviación estándar, el cambio en puntos del jugador para el evento, y, despues del simbolo de igualdad («=»), el rating y la desviación estándar final. A continuación sigue el número de juegos ganados y perdidos por el jugador.
El valor en la columna del jugador contrincante («Opponent!s Rating») es la media y la desviación estándar de la ley de ajuste del contrincante. Como mencionamos anteriormente, el sistema de rating usa diferentes leyes de ajustes para el mismo contrincante cuando juega contra jugadores diferentes. Por ejemplo, el rating (ajustado) de Claude Boulardel es 1761±43 cuando el jugó contra Alex Landsman, pero 1771±42 cuando jugo contra Chris Kalagher.
El valor en la columna de cambio de punto («Point Change») es el cambio de punto para el jugador a consecuencia del resultado de ese partido. El sistema procesa como una unidad los varios partidos jugados entre los dos mismos jugadores. En este caso, el cambio de punto total que publicamos para todos los partidos entre los mismos jugadores es distribuido a los partidos siguiendo estas reglas:
- Si el cambio de punto total es positivo (o cero), entonces el cambio de punto total es distribuido en partes iguales a los partidos que el jugador ganó; y entonces el cambio de punto de cada partido que el jugador perdió es cero.
- Si el cambio de punto total es negativo, entonces el cambio de punto total es distribuido en partes iguales a los partidos que el jugador perdió; y asigna un cero a aquellos cambios de punto a los partidos que el jugador ganó.
Si los dos jugadores jugaron más de dos partidos entre ellos, habrá un asterisco después del valor de cambio de puntos. Por ejemplo, Claude Boulard ganó un total de 14 puntos total por un partido que ganó y uno que perdió contra Sonu Bhatia. Claude también ganó un total de 26 puntos por sus dos partidos ganados contra Alex Landsman.
El cambio de punto por partido depende del orden en que el sistema procesa los datos de los partidos. Así que, los valores reportados como el cambio de puntos son más bien sugerencias. Sin embargo, la suma de los cambios de punto para cada partido es igual al total de cambios de puntos para el jugador en el evento, y este total no depende del orden de procesamiento de los datos de los partidos que el sistema utiliza.
La dependencia del cambio de puntos por partido a la orden de procesamiento tiene sentido intuitivo. Supón que vemos un jugador de rating 2000 ganarle a un jugador de rating 2200 (o sea un resultado inesperado). En este caso le damos un aumento significante al jugador ganador, ya que es un resultado inesperado. Ahora, supón que vemos este mismo jugador ganarle a otro jugador de 2200. Entonces aquí aumentamos el estimado del rating del jugador ganador, pero no por la misma cantidad que el juego anterior.
Para facilitar el entendimiento del reporte detallado, los partidos están clasificados en el siguiente orden: Primero las perdidas en orden ascendente del rating del contrincante. A continuación las victorias en orden descendente del rating del contrincante. Si el jugador tiene ambos resultados, una victoria y una derrota, contra un contrincante con rating superior los partidos serán clasificados como una victoria, por el contrario serán clasificados como una perdida.
El numero de puntos ganados por el ganador de un partido casi nunca es igual al numero de puntos rebajados del perdedor de ese partido. Por ejemplo, Claude Boulard ganó un total de 26 puntos por sus dos victorias contra Alex Landsman, pero Alex perdió 44 puntos por esos dos partidos. En este caso, Alex perdió más puntos porque la desviación estándar de la ley de Alex es mucho más alta que la de Claude; y la media de Alex y Claude son similares después de procesar los datos de los otros partidos jugados.
En el web, los valores de cambio de puntos son redondeados a una cifra entera. Por consecuencia, ocasionalmente la suma de los cambio de puntos por partido no es igual que el cambio de puntos total del evento para cada jugador. Si hay alguna discrepancia, usualmente no excede a un punto.
Referencias
Marcus, David J. (2001) New Table-Tennis Rating System. Journal of the Royal Statistical Society: Series D (The Statistician), 50: 191–208. doi: 10.1111/1467-9884.00271
Marcus, David J. (2011a) Ratings Central: Accurate, Automated, Bayesian Table Tennis Ratings for Clubs, Leagues, Tournaments, and Organizations. Joint Statistical Meetings, July 30–August 4, 2011.
Marcus, David J. (2011b) Ratings Central: Accurate, Automated, Bayesian Table Tennis Ratings for Clubs, Leagues, Tournaments, and Organizations. NESSIS (New England Symposium on Statistics in Sports), September 24, 2011.
Marcus, David J. (2023) Long-Term Stable, Quick-Reacting Table Tennis Ratings via Poisson Jumps. September 24, 2023; revised July 27, 2025.
Traducción al español por Alberto Calvo.

